Por código, a forma mais eficiente de verificar se um ponto está sobre um círculo é calculando se a distância entre o ponto e o centro do círculo é menor ou igual ao raio.
Neste exemplo, posicionamos na tela dois círculos de raio e posições aleatórias e fazemos esta verificação para um deles.
sábado, 20 de setembro de 2014
Trabalho 01 - Proporção áurea
A proporção áurea é uma constante matemática conhecida desde a antiguidade. Seu valor é comumente arredondado para 1,618 e sua representação é a letra grega phi, em homenagem ao escultor grego Phideas, que teria concebido o Partenon, em Atenas.
Existe certo misticismo sobre este número por estar presente em diversas estruturas naturais e obras clássicas de todo o mundo, o que lhe cunhou a denominação de proporção divina.
Esta constante deriva-se da sequência de Fibonacci, a conhecida sucessão de inteiros onde cada número é a soma dos dois anteriores: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34... Quando se divide um número de Fibonacci pelo seu antecessor, obtém-se um produto próximo à proporção áurea. Na verdade, quanto maiores os números escolhidos, mais próximo o resultado:
Fibonacci é o nome pelo qual é conhecido o matemático italiano Leonardo de Pisa, que tornou a sucessão popular na Europa no século XII ao utilizá-la em uma de suas obras escritas. Observemos a proporção áurea mais uma vez, agora na natureza:
A comunidade OpenProcessing tem diversos exemplos relacionados à proporção áurea desenvolvidos com Processing. Analisemos a relação entre os modelos natural e matemático da disposição das sementes de girassol que resultam no modelo computacional obtido neste sketch:
As sementes do girassol formam arcos em uma estrutura notável:
Outras espécies de plantas apresentam estrutura similar, como a margarida.
MODELO MATEMÁTICO
Como destacado anteriormente, os arcos cruzados que se formam através desta disposição específica crescem segundo a razão áurea. O modelo matemático que descreve este crescimento utiliza a constante phi. Cada semente nasce em um ângulo de aproximadamente 137,5° em relação à anterior. Este valor é o resultado da divisão de uma volta completa (360°) por phi (1,618...) subtraído de uma volta completa:
MODELO COMPUTACIONAL
Para tornar o exemplo escolhido mais compreensível, reformulei e comentei e código:
No código reformulado, explico detalhadamente a construção do modelo computacional. Aqui no blog, comentarei apenas os resultados observados.
No sketch escolhido, o autor não torna explícito o modelo matemático, mas utiliza o resultado: a cada iteração, rotaciona-se a referência da tela em 137,5° para desenhar a próxima semente (linha 11 no código original). A semente se distancia do centro da estrutura a cada frame, representando a passagem do tempo.
Para melhor visualização, modifiquei o exemplo para exibir apenas as 3 primeiras sementes. Após determinado tempo, obtemos esta disposição:
Essa sequência de ângulos se repete até formar a estrutura completa das sementes:
Este modelo computacional gera um produto gráfico atraente e de fácil compreensão por conta da animação e da separação espacial de cada "semente". Mas existe um outro modelo mais completo e flexível que nos permite explorar outras possibilidades a partir do mesmo modelo matemático.
MODELO COMPUTACIONAL 2
Este segundo modelo utiliza os mesmo princípios do primeiro, mas oferece variáveis de controle, o que permite experimentos muito mais variados. As variáveis relevantes são definidas nas últimas 4 linhas do setup:
Modificando a razão de crescimento (rgrowth) de 1,004 para 1,008, conseguimos 13 e 21 espirais:
A razão de crescimento modifica a velocidade com que as sementes se distanciam do centro da estrutura. Valores maiores fazem as sementes se afastar mais rápido, a estrutura fica "aberta" e comporta menos espirais. Pode-se concluir então que a quantidade de espirais na estrutura depende da velocidade de crescimento da flor.
Retornando a razão de crescimento ao valor original, podemos fazer outros testes interessantes. Se modificarmos a distância angular entre as sementes em 1 grau para mais ou para menos, o resultado é visivelmente diferente do natural:
E se utilizarmos outra constante no lugar do phi, como o pi (3,1415...):
FONTES
 |
| Letra grega phi maiúscula |
Existe certo misticismo sobre este número por estar presente em diversas estruturas naturais e obras clássicas de todo o mundo, o que lhe cunhou a denominação de proporção divina.
 |
| A Grande Pirâmide de Gizé tem a razão áurea entre a lateral e metade da base |
 |
| O templo Partenon usa a proporção de ouro várias vezes |
Esta constante deriva-se da sequência de Fibonacci, a conhecida sucessão de inteiros onde cada número é a soma dos dois anteriores: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34... Quando se divide um número de Fibonacci pelo seu antecessor, obtém-se um produto próximo à proporção áurea. Na verdade, quanto maiores os números escolhidos, mais próximo o resultado:
Fibonacci é o nome pelo qual é conhecido o matemático italiano Leonardo de Pisa, que tornou a sucessão popular na Europa no século XII ao utilizá-la em uma de suas obras escritas. Observemos a proporção áurea mais uma vez, agora na natureza:
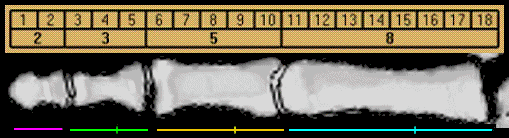 | |
| O dedo humano tem proporções que seguem a sequência de Fibonacci e, portanto, a razão áurea |
 | |
| As linhas da espiral de sementes do girassol crescem em razão áurea: a diferença de tamanho entre os arcos destacados segue a sequência de Fibonacci |
A comunidade OpenProcessing tem diversos exemplos relacionados à proporção áurea desenvolvidos com Processing. Analisemos a relação entre os modelos natural e matemático da disposição das sementes de girassol que resultam no modelo computacional obtido neste sketch:
MODELO NATURAL
As sementes do girassol formam arcos em uma estrutura notável:
Outras espécies de plantas apresentam estrutura similar, como a margarida.
MODELO MATEMÁTICO
Como destacado anteriormente, os arcos cruzados que se formam através desta disposição específica crescem segundo a razão áurea. O modelo matemático que descreve este crescimento utiliza a constante phi. Cada semente nasce em um ângulo de aproximadamente 137,5° em relação à anterior. Este valor é o resultado da divisão de uma volta completa (360°) por phi (1,618...) subtraído de uma volta completa:
MODELO COMPUTACIONAL
Para tornar o exemplo escolhido mais compreensível, reformulei e comentei e código:
No código reformulado, explico detalhadamente a construção do modelo computacional. Aqui no blog, comentarei apenas os resultados observados.
No sketch escolhido, o autor não torna explícito o modelo matemático, mas utiliza o resultado: a cada iteração, rotaciona-se a referência da tela em 137,5° para desenhar a próxima semente (linha 11 no código original). A semente se distancia do centro da estrutura a cada frame, representando a passagem do tempo.
Para melhor visualização, modifiquei o exemplo para exibir apenas as 3 primeiras sementes. Após determinado tempo, obtemos esta disposição:
Essa sequência de ângulos se repete até formar a estrutura completa das sementes:
Este modelo computacional gera um produto gráfico atraente e de fácil compreensão por conta da animação e da separação espacial de cada "semente". Mas existe um outro modelo mais completo e flexível que nos permite explorar outras possibilidades a partir do mesmo modelo matemático.
MODELO COMPUTACIONAL 2
Este segundo modelo utiliza os mesmo princípios do primeiro, mas oferece variáveis de controle, o que permite experimentos muito mais variados. As variáveis relevantes são definidas nas últimas 4 linhas do setup:
- g: golden ratio, ou razão áurea
- gAng: golden angle, o ângulo obtido a partir do modelo matemático já apresentado
- rad: radius, o raio tomado como base para a estrutura das sementes
- rgrowth: growth reason, a razão de crescimento da estrutura, aumenta a distância entre as sementes e o centro da estrutura
O resultado é este:
Este resultado gera 21 espirais em sentido horário e 34 em anti-horário (números de Fibonacci), exatamente a quantidade de espirais da margarida. O modelo anterior tinha 13 e 21 espirais, respectivamente. Por que ocorre esta diferença, já que usamos o mesmo modelo matemático?
 |
| A margarida tem 21 espirais de sementes em sentido horário e 31 em anti-horário |
Modificando a razão de crescimento (rgrowth) de 1,004 para 1,008, conseguimos 13 e 21 espirais:
A razão de crescimento modifica a velocidade com que as sementes se distanciam do centro da estrutura. Valores maiores fazem as sementes se afastar mais rápido, a estrutura fica "aberta" e comporta menos espirais. Pode-se concluir então que a quantidade de espirais na estrutura depende da velocidade de crescimento da flor.
Retornando a razão de crescimento ao valor original, podemos fazer outros testes interessantes. Se modificarmos a distância angular entre as sementes em 1 grau para mais ou para menos, o resultado é visivelmente diferente do natural:
E se utilizarmos outra constante no lugar do phi, como o pi (3,1415...):
FONTES
quinta-feira, 4 de setembro de 2014
Aula 10 - Construções geométricas
Via de regra, logos profissionais são desenvolvidas a partir de modelos matemáticos. Note-se os exemplos abaixo.
Ambos utilizam vários arcos e círculos em sua construção. A construção destas logo é um processo de sobreposição de várias camadas de cores positiva e negativa. No exemplo do Twitter, pode-se considerar o azul como positivo e o branco como negativo.
Utilizando o mesmo processo é possivel recriar o símbolo Yin-Yang a partir deste modelo:
Existem outros modelos matemáticos do Yin-Yang, mas este me parece o mais simples e exato.
Utilizando as funções de arco do Processing, pode-se quebrar o símbolo em dois arcos escuros e dois claros. Os círculos menores contrastantes são elipses.
Resultado final:
 |
| Apple |
 |
Utilizando o mesmo processo é possivel recriar o símbolo Yin-Yang a partir deste modelo:
Existem outros modelos matemáticos do Yin-Yang, mas este me parece o mais simples e exato.
Utilizando as funções de arco do Processing, pode-se quebrar o símbolo em dois arcos escuros e dois claros. Os círculos menores contrastantes são elipses.
 |
| Contraste de tons para melhor visualização dos arcos e círculos |
Resultado final:
terça-feira, 2 de setembro de 2014
Aula 09 - Breakout: colisão
O jogo Breakout foi lançado poucos anos depois do Pong e deriva características deste jogo: a movimentação da bola e da raquete são quase iguais. A diferença técnica consiste no objetivo (destruir todos os tijolos na tela), no eixo da raquete (horizontal), na área de escape da bola (apenas embaixo) e no fato de cada partida ser para um único jogador.
Continuando o trabalho da aula do Pong, implementamos um mecanismo de colisão: verificamos se determinado ponto está dentro da área de um retângulo. Este mecanismo é, na verdade, a combinação de uma série de condições: se o valor X do ponto é maior que a extremidade esquerda e menor que a extremidade direita do retângulo e o valor Y é maior que a extremidade superior e menor que a inferior, então o ponto está inserido no retângulo.
O ponto que tratamos é a extremidade inferior da bola do Breakout, e o retângulo é a raquete do jogador. Quando esta condição é verdadeira, ou seja, a bola encostou na raquete, invertemos a velocidade Y da bola para que ela rebata.
Para deixar o jogo mais interessante, a velocidade da bola sofre um efeito ao rebater na raquete: se a raquete se move em sentido contrário ao da bola, a velocidade horizontal diminui; do contrário, aumenta.
Continuando o trabalho da aula do Pong, implementamos um mecanismo de colisão: verificamos se determinado ponto está dentro da área de um retângulo. Este mecanismo é, na verdade, a combinação de uma série de condições: se o valor X do ponto é maior que a extremidade esquerda e menor que a extremidade direita do retângulo e o valor Y é maior que a extremidade superior e menor que a inferior, então o ponto está inserido no retângulo.
O ponto que tratamos é a extremidade inferior da bola do Breakout, e o retângulo é a raquete do jogador. Quando esta condição é verdadeira, ou seja, a bola encostou na raquete, invertemos a velocidade Y da bola para que ela rebata.
Para deixar o jogo mais interessante, a velocidade da bola sofre um efeito ao rebater na raquete: se a raquete se move em sentido contrário ao da bola, a velocidade horizontal diminui; do contrário, aumenta.
Aula 08 - Pong
Reconhecido como o primeiro videogame lucrativo da história, o Pong foi criado na década de 70 e "bombou" ao ser lançado pela Atari. O jogo é disputado por duas pessoas e se resume a uma tela preta com dois paddles e uma bola branca que rebate.
Na aula 8 de MAM, reproduzimos o movimento básico da bola do Pong.
O movimento é comandando por duas variáveis: velocidade horizontal e vertical da bola. Cada vez que a bola atinge o limite da tela na horizontal, a velocidade horizontal se inverte (multiplica-se por -1) e aumenta em 10% (multiplica-se por 1,1). O mesmo acontece para a velocidade vertical ao atingir a parte de cima ou de baixo da tela.
Após certo tempo, a velocidade teria um valor tão alto que o deslocamento da bola extrapolaria a área da tela, sendo impossível vê-la. Para evitar isto, acrescentei uma condição para impedir o aumento de velocidade a partir de 50 pixels por frame.
Por fim, adicionamos um paddle que segue o cursor do mouse, ainda sem mecanismo de colisão, para continuação na próxima aula. O tracejado que divide a tela é gerado por um laço de repetição que desenha uma linha de pequenos quadrados.
Na aula 8 de MAM, reproduzimos o movimento básico da bola do Pong.
O movimento é comandando por duas variáveis: velocidade horizontal e vertical da bola. Cada vez que a bola atinge o limite da tela na horizontal, a velocidade horizontal se inverte (multiplica-se por -1) e aumenta em 10% (multiplica-se por 1,1). O mesmo acontece para a velocidade vertical ao atingir a parte de cima ou de baixo da tela.
Após certo tempo, a velocidade teria um valor tão alto que o deslocamento da bola extrapolaria a área da tela, sendo impossível vê-la. Para evitar isto, acrescentei uma condição para impedir o aumento de velocidade a partir de 50 pixels por frame.
Por fim, adicionamos um paddle que segue o cursor do mouse, ainda sem mecanismo de colisão, para continuação na próxima aula. O tracejado que divide a tela é gerado por um laço de repetição que desenha uma linha de pequenos quadrados.
Aula 07 - Relógio: resto e quociente
O desafio é criar um relógio usando o Pebble Alphabet de Clotilde Olyff.
Para isto, podemos extrair os algarismos da imagem acima manualmente e salvá-los como imagens individuais. Então, no sketch, quando quisermos exibir o dígito "1", por exemplo, carregamos a imagem respectiva e exibimos na tela.
O Processing oferece funções para capturar horas, minutos e segundos do sistema na forma de números inteiros. Porém para exibir os dígitos corretos conforme explicado anteriormente é preciso quebrar os números de dois algarismos em dígitos individuais. "12", por exemplo, deve ser quebrado em "1" e "2".
A solução é simples: dividir o inteiro por 10. Mantendo "12" como exemplo, o quociente da divisão será "1", e o resto será "2". Temos os dígitos necessários: "1" e "2". Isto é feito para horas, minutos e segundos. O resultado é este:
Como este arquivo envolve carregamento de imagens, não é possível executá-lo online.
Para isto, podemos extrair os algarismos da imagem acima manualmente e salvá-los como imagens individuais. Então, no sketch, quando quisermos exibir o dígito "1", por exemplo, carregamos a imagem respectiva e exibimos na tela.
O Processing oferece funções para capturar horas, minutos e segundos do sistema na forma de números inteiros. Porém para exibir os dígitos corretos conforme explicado anteriormente é preciso quebrar os números de dois algarismos em dígitos individuais. "12", por exemplo, deve ser quebrado em "1" e "2".
A solução é simples: dividir o inteiro por 10. Mantendo "12" como exemplo, o quociente da divisão será "1", e o resto será "2". Temos os dígitos necessários: "1" e "2". Isto é feito para horas, minutos e segundos. O resultado é este:
Como este arquivo envolve carregamento de imagens, não é possível executá-lo online.
Assinar:
Comentários (Atom)



















