Fade é uma técnica de suavização de transição de imagens (do preto, do branco ou de outra imagem). Quando o fade se origina de uma outra imagem, diz-se que o efeito é de crossfade.
O efeito é obtido alterando o peso de uma média ponderada (alpha) entre a cor de cada pixel das duas imagens. No início da transição, o peso é de 100% para a primeira imagem. No meio, o peso é de 50% para cada imagem. No final, 100% para a segunda imagem.
Para obter efeitos variados de crossfade, pode-se variar a velocidade de mudança do peso (alpha), utilizando uma função senóide, por exemplo. A demonstração abaixo utiliza transição linear, no entanto.
domingo, 23 de novembro de 2014
domingo, 16 de novembro de 2014
Trabalho Final - Espirógrafo
Funções trigonométricas regem muitos -- se não a maioria -- dos movimentos oscilatórios naturais, desde o balanço de um pêndulo até o traçado de alguém caminhando.
Elas regem também as possibilidades fantásticas obtidas pelo desenho no espirógrafo:
O espirógrafo foi inventado por um engenheiro britânico em 1965 e hoje tem os direitos reservados pela Hasbro. Existem variações mecânicas do brinquedo, mas o original consiste em um conjunto de engrenagens encaixáveis, sendo uma delas em forma de círculo (com dentes internos) e a outra em forma de moeda (com dentes externos) com perfurações.
Para usá-lo, você deve colocar o par de engrenagens sobre um papel, inserir uma caneta em uma das perfurações da engrenagem-moeda e girá-la por dentro da engrenagem-círculo.
Para reproduzir este movimento no Processing, longe de executar cálculos físicos para obter o o movimento dos dentes das engrenagens, utilizei funções trigonométricas simples para determinar posição correta da engrenagem e do traço.
A partir daqui, chamarei a engrenagem-círculo de Círculo, a engrenagem-moeda de Engrenagem, e a perfuração na engrenagem-moeda de Ponto.
A Engrenagem faz um movimento circular contínuo em torno do centro do Círculo, calculado utilizando coordenadas polares e funções de seno e cosseno. O raio da Engrenagem pode ser alterado pelo usuário, mas ela sempre deve tocar a borda do Círculo. Para obter este resultado, a distância utilizada no cálculo da coordenada polar é o raio do Círculo menos o raio da Engrenagem. A posição obtida no cálculo é função do cosseno (horizontal) e seno (vertical) do ângulo atual.
Devemos notar que, se a Engrenagem translada em sentido horário, sua rotação será em sentido anti-horário. Portanto, o Ponto sobre a Engrenagem gira no sentido contrário à velocidade angular de translação da Engrenagem.
A posição correta do Ponto é calculado pelo mesmo processo de coordenadas polares da posição da Engrenagem, utilizando a distância, o centro e o raio da Engrenagem como parâmetros.
Resumindo, executo dois cálculos de coordenadas polares: da Engrenagem em relação ao Círculo, e depois do Ponto em relação à Engrenagem, conforme a animação acima.
Por fim, acrescentei controles para parametrizar raios e distâncias diversos utilizando a biblioteca de interface gráfica ControlP5.
Veja a demonstração do Espirógrafo concluído:
Obs.: é necessário ter a biblioteca ControlP5 para executar este sketch, em Sketch >> Import Library... >> Add Library... >> ControlP5
Elas regem também as possibilidades fantásticas obtidas pelo desenho no espirógrafo:
 |
| Desenhos feitos com lápis colorido em um espirógrafo |
 |
| Desenhando em um espirógrafo |
Para usá-lo, você deve colocar o par de engrenagens sobre um papel, inserir uma caneta em uma das perfurações da engrenagem-moeda e girá-la por dentro da engrenagem-círculo.
Para reproduzir este movimento no Processing, longe de executar cálculos físicos para obter o o movimento dos dentes das engrenagens, utilizei funções trigonométricas simples para determinar posição correta da engrenagem e do traço.
A partir daqui, chamarei a engrenagem-círculo de Círculo, a engrenagem-moeda de Engrenagem, e a perfuração na engrenagem-moeda de Ponto.
A Engrenagem faz um movimento circular contínuo em torno do centro do Círculo, calculado utilizando coordenadas polares e funções de seno e cosseno. O raio da Engrenagem pode ser alterado pelo usuário, mas ela sempre deve tocar a borda do Círculo. Para obter este resultado, a distância utilizada no cálculo da coordenada polar é o raio do Círculo menos o raio da Engrenagem. A posição obtida no cálculo é função do cosseno (horizontal) e seno (vertical) do ângulo atual.
Devemos notar que, se a Engrenagem translada em sentido horário, sua rotação será em sentido anti-horário. Portanto, o Ponto sobre a Engrenagem gira no sentido contrário à velocidade angular de translação da Engrenagem.
A posição correta do Ponto é calculado pelo mesmo processo de coordenadas polares da posição da Engrenagem, utilizando a distância, o centro e o raio da Engrenagem como parâmetros.
Resumindo, executo dois cálculos de coordenadas polares: da Engrenagem em relação ao Círculo, e depois do Ponto em relação à Engrenagem, conforme a animação acima.
Por fim, acrescentei controles para parametrizar raios e distâncias diversos utilizando a biblioteca de interface gráfica ControlP5.
Veja a demonstração do Espirógrafo concluído:
Obs.: é necessário ter a biblioteca ControlP5 para executar este sketch, em Sketch >> Import Library... >> Add Library... >> ControlP5
sábado, 20 de setembro de 2014
Aula 12 - Colisão em círculos
Por código, a forma mais eficiente de verificar se um ponto está sobre um círculo é calculando se a distância entre o ponto e o centro do círculo é menor ou igual ao raio.
Neste exemplo, posicionamos na tela dois círculos de raio e posições aleatórias e fazemos esta verificação para um deles.
Neste exemplo, posicionamos na tela dois círculos de raio e posições aleatórias e fazemos esta verificação para um deles.
Trabalho 01 - Proporção áurea
A proporção áurea é uma constante matemática conhecida desde a antiguidade. Seu valor é comumente arredondado para 1,618 e sua representação é a letra grega phi, em homenagem ao escultor grego Phideas, que teria concebido o Partenon, em Atenas.
Existe certo misticismo sobre este número por estar presente em diversas estruturas naturais e obras clássicas de todo o mundo, o que lhe cunhou a denominação de proporção divina.
Esta constante deriva-se da sequência de Fibonacci, a conhecida sucessão de inteiros onde cada número é a soma dos dois anteriores: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34... Quando se divide um número de Fibonacci pelo seu antecessor, obtém-se um produto próximo à proporção áurea. Na verdade, quanto maiores os números escolhidos, mais próximo o resultado:
Fibonacci é o nome pelo qual é conhecido o matemático italiano Leonardo de Pisa, que tornou a sucessão popular na Europa no século XII ao utilizá-la em uma de suas obras escritas. Observemos a proporção áurea mais uma vez, agora na natureza:
A comunidade OpenProcessing tem diversos exemplos relacionados à proporção áurea desenvolvidos com Processing. Analisemos a relação entre os modelos natural e matemático da disposição das sementes de girassol que resultam no modelo computacional obtido neste sketch:
As sementes do girassol formam arcos em uma estrutura notável:
Outras espécies de plantas apresentam estrutura similar, como a margarida.
MODELO MATEMÁTICO
Como destacado anteriormente, os arcos cruzados que se formam através desta disposição específica crescem segundo a razão áurea. O modelo matemático que descreve este crescimento utiliza a constante phi. Cada semente nasce em um ângulo de aproximadamente 137,5° em relação à anterior. Este valor é o resultado da divisão de uma volta completa (360°) por phi (1,618...) subtraído de uma volta completa:
MODELO COMPUTACIONAL
Para tornar o exemplo escolhido mais compreensível, reformulei e comentei e código:
No código reformulado, explico detalhadamente a construção do modelo computacional. Aqui no blog, comentarei apenas os resultados observados.
No sketch escolhido, o autor não torna explícito o modelo matemático, mas utiliza o resultado: a cada iteração, rotaciona-se a referência da tela em 137,5° para desenhar a próxima semente (linha 11 no código original). A semente se distancia do centro da estrutura a cada frame, representando a passagem do tempo.
Para melhor visualização, modifiquei o exemplo para exibir apenas as 3 primeiras sementes. Após determinado tempo, obtemos esta disposição:
Essa sequência de ângulos se repete até formar a estrutura completa das sementes:
Este modelo computacional gera um produto gráfico atraente e de fácil compreensão por conta da animação e da separação espacial de cada "semente". Mas existe um outro modelo mais completo e flexível que nos permite explorar outras possibilidades a partir do mesmo modelo matemático.
MODELO COMPUTACIONAL 2
Este segundo modelo utiliza os mesmo princípios do primeiro, mas oferece variáveis de controle, o que permite experimentos muito mais variados. As variáveis relevantes são definidas nas últimas 4 linhas do setup:
Modificando a razão de crescimento (rgrowth) de 1,004 para 1,008, conseguimos 13 e 21 espirais:
A razão de crescimento modifica a velocidade com que as sementes se distanciam do centro da estrutura. Valores maiores fazem as sementes se afastar mais rápido, a estrutura fica "aberta" e comporta menos espirais. Pode-se concluir então que a quantidade de espirais na estrutura depende da velocidade de crescimento da flor.
Retornando a razão de crescimento ao valor original, podemos fazer outros testes interessantes. Se modificarmos a distância angular entre as sementes em 1 grau para mais ou para menos, o resultado é visivelmente diferente do natural:
E se utilizarmos outra constante no lugar do phi, como o pi (3,1415...):
FONTES
 |
| Letra grega phi maiúscula |
Existe certo misticismo sobre este número por estar presente em diversas estruturas naturais e obras clássicas de todo o mundo, o que lhe cunhou a denominação de proporção divina.
 |
| A Grande Pirâmide de Gizé tem a razão áurea entre a lateral e metade da base |
 |
| O templo Partenon usa a proporção de ouro várias vezes |
Esta constante deriva-se da sequência de Fibonacci, a conhecida sucessão de inteiros onde cada número é a soma dos dois anteriores: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34... Quando se divide um número de Fibonacci pelo seu antecessor, obtém-se um produto próximo à proporção áurea. Na verdade, quanto maiores os números escolhidos, mais próximo o resultado:
Fibonacci é o nome pelo qual é conhecido o matemático italiano Leonardo de Pisa, que tornou a sucessão popular na Europa no século XII ao utilizá-la em uma de suas obras escritas. Observemos a proporção áurea mais uma vez, agora na natureza:
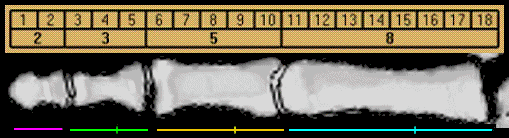 | |
| O dedo humano tem proporções que seguem a sequência de Fibonacci e, portanto, a razão áurea |
 | |
| As linhas da espiral de sementes do girassol crescem em razão áurea: a diferença de tamanho entre os arcos destacados segue a sequência de Fibonacci |
A comunidade OpenProcessing tem diversos exemplos relacionados à proporção áurea desenvolvidos com Processing. Analisemos a relação entre os modelos natural e matemático da disposição das sementes de girassol que resultam no modelo computacional obtido neste sketch:
MODELO NATURAL
As sementes do girassol formam arcos em uma estrutura notável:
Outras espécies de plantas apresentam estrutura similar, como a margarida.
MODELO MATEMÁTICO
Como destacado anteriormente, os arcos cruzados que se formam através desta disposição específica crescem segundo a razão áurea. O modelo matemático que descreve este crescimento utiliza a constante phi. Cada semente nasce em um ângulo de aproximadamente 137,5° em relação à anterior. Este valor é o resultado da divisão de uma volta completa (360°) por phi (1,618...) subtraído de uma volta completa:
MODELO COMPUTACIONAL
Para tornar o exemplo escolhido mais compreensível, reformulei e comentei e código:
No código reformulado, explico detalhadamente a construção do modelo computacional. Aqui no blog, comentarei apenas os resultados observados.
No sketch escolhido, o autor não torna explícito o modelo matemático, mas utiliza o resultado: a cada iteração, rotaciona-se a referência da tela em 137,5° para desenhar a próxima semente (linha 11 no código original). A semente se distancia do centro da estrutura a cada frame, representando a passagem do tempo.
Para melhor visualização, modifiquei o exemplo para exibir apenas as 3 primeiras sementes. Após determinado tempo, obtemos esta disposição:
Essa sequência de ângulos se repete até formar a estrutura completa das sementes:
Este modelo computacional gera um produto gráfico atraente e de fácil compreensão por conta da animação e da separação espacial de cada "semente". Mas existe um outro modelo mais completo e flexível que nos permite explorar outras possibilidades a partir do mesmo modelo matemático.
MODELO COMPUTACIONAL 2
Este segundo modelo utiliza os mesmo princípios do primeiro, mas oferece variáveis de controle, o que permite experimentos muito mais variados. As variáveis relevantes são definidas nas últimas 4 linhas do setup:
- g: golden ratio, ou razão áurea
- gAng: golden angle, o ângulo obtido a partir do modelo matemático já apresentado
- rad: radius, o raio tomado como base para a estrutura das sementes
- rgrowth: growth reason, a razão de crescimento da estrutura, aumenta a distância entre as sementes e o centro da estrutura
O resultado é este:
Este resultado gera 21 espirais em sentido horário e 34 em anti-horário (números de Fibonacci), exatamente a quantidade de espirais da margarida. O modelo anterior tinha 13 e 21 espirais, respectivamente. Por que ocorre esta diferença, já que usamos o mesmo modelo matemático?
 |
| A margarida tem 21 espirais de sementes em sentido horário e 31 em anti-horário |
Modificando a razão de crescimento (rgrowth) de 1,004 para 1,008, conseguimos 13 e 21 espirais:
A razão de crescimento modifica a velocidade com que as sementes se distanciam do centro da estrutura. Valores maiores fazem as sementes se afastar mais rápido, a estrutura fica "aberta" e comporta menos espirais. Pode-se concluir então que a quantidade de espirais na estrutura depende da velocidade de crescimento da flor.
Retornando a razão de crescimento ao valor original, podemos fazer outros testes interessantes. Se modificarmos a distância angular entre as sementes em 1 grau para mais ou para menos, o resultado é visivelmente diferente do natural:
E se utilizarmos outra constante no lugar do phi, como o pi (3,1415...):
FONTES
quinta-feira, 4 de setembro de 2014
Aula 10 - Construções geométricas
Via de regra, logos profissionais são desenvolvidas a partir de modelos matemáticos. Note-se os exemplos abaixo.
Ambos utilizam vários arcos e círculos em sua construção. A construção destas logo é um processo de sobreposição de várias camadas de cores positiva e negativa. No exemplo do Twitter, pode-se considerar o azul como positivo e o branco como negativo.
Utilizando o mesmo processo é possivel recriar o símbolo Yin-Yang a partir deste modelo:
Existem outros modelos matemáticos do Yin-Yang, mas este me parece o mais simples e exato.
Utilizando as funções de arco do Processing, pode-se quebrar o símbolo em dois arcos escuros e dois claros. Os círculos menores contrastantes são elipses.
Resultado final:
 |
| Apple |
 |
Utilizando o mesmo processo é possivel recriar o símbolo Yin-Yang a partir deste modelo:
Existem outros modelos matemáticos do Yin-Yang, mas este me parece o mais simples e exato.
Utilizando as funções de arco do Processing, pode-se quebrar o símbolo em dois arcos escuros e dois claros. Os círculos menores contrastantes são elipses.
 |
| Contraste de tons para melhor visualização dos arcos e círculos |
Resultado final:
terça-feira, 2 de setembro de 2014
Aula 09 - Breakout: colisão
O jogo Breakout foi lançado poucos anos depois do Pong e deriva características deste jogo: a movimentação da bola e da raquete são quase iguais. A diferença técnica consiste no objetivo (destruir todos os tijolos na tela), no eixo da raquete (horizontal), na área de escape da bola (apenas embaixo) e no fato de cada partida ser para um único jogador.
Continuando o trabalho da aula do Pong, implementamos um mecanismo de colisão: verificamos se determinado ponto está dentro da área de um retângulo. Este mecanismo é, na verdade, a combinação de uma série de condições: se o valor X do ponto é maior que a extremidade esquerda e menor que a extremidade direita do retângulo e o valor Y é maior que a extremidade superior e menor que a inferior, então o ponto está inserido no retângulo.
O ponto que tratamos é a extremidade inferior da bola do Breakout, e o retângulo é a raquete do jogador. Quando esta condição é verdadeira, ou seja, a bola encostou na raquete, invertemos a velocidade Y da bola para que ela rebata.
Para deixar o jogo mais interessante, a velocidade da bola sofre um efeito ao rebater na raquete: se a raquete se move em sentido contrário ao da bola, a velocidade horizontal diminui; do contrário, aumenta.
Continuando o trabalho da aula do Pong, implementamos um mecanismo de colisão: verificamos se determinado ponto está dentro da área de um retângulo. Este mecanismo é, na verdade, a combinação de uma série de condições: se o valor X do ponto é maior que a extremidade esquerda e menor que a extremidade direita do retângulo e o valor Y é maior que a extremidade superior e menor que a inferior, então o ponto está inserido no retângulo.
O ponto que tratamos é a extremidade inferior da bola do Breakout, e o retângulo é a raquete do jogador. Quando esta condição é verdadeira, ou seja, a bola encostou na raquete, invertemos a velocidade Y da bola para que ela rebata.
Para deixar o jogo mais interessante, a velocidade da bola sofre um efeito ao rebater na raquete: se a raquete se move em sentido contrário ao da bola, a velocidade horizontal diminui; do contrário, aumenta.
Aula 08 - Pong
Reconhecido como o primeiro videogame lucrativo da história, o Pong foi criado na década de 70 e "bombou" ao ser lançado pela Atari. O jogo é disputado por duas pessoas e se resume a uma tela preta com dois paddles e uma bola branca que rebate.
Na aula 8 de MAM, reproduzimos o movimento básico da bola do Pong.
O movimento é comandando por duas variáveis: velocidade horizontal e vertical da bola. Cada vez que a bola atinge o limite da tela na horizontal, a velocidade horizontal se inverte (multiplica-se por -1) e aumenta em 10% (multiplica-se por 1,1). O mesmo acontece para a velocidade vertical ao atingir a parte de cima ou de baixo da tela.
Após certo tempo, a velocidade teria um valor tão alto que o deslocamento da bola extrapolaria a área da tela, sendo impossível vê-la. Para evitar isto, acrescentei uma condição para impedir o aumento de velocidade a partir de 50 pixels por frame.
Por fim, adicionamos um paddle que segue o cursor do mouse, ainda sem mecanismo de colisão, para continuação na próxima aula. O tracejado que divide a tela é gerado por um laço de repetição que desenha uma linha de pequenos quadrados.
Na aula 8 de MAM, reproduzimos o movimento básico da bola do Pong.
O movimento é comandando por duas variáveis: velocidade horizontal e vertical da bola. Cada vez que a bola atinge o limite da tela na horizontal, a velocidade horizontal se inverte (multiplica-se por -1) e aumenta em 10% (multiplica-se por 1,1). O mesmo acontece para a velocidade vertical ao atingir a parte de cima ou de baixo da tela.
Após certo tempo, a velocidade teria um valor tão alto que o deslocamento da bola extrapolaria a área da tela, sendo impossível vê-la. Para evitar isto, acrescentei uma condição para impedir o aumento de velocidade a partir de 50 pixels por frame.
Por fim, adicionamos um paddle que segue o cursor do mouse, ainda sem mecanismo de colisão, para continuação na próxima aula. O tracejado que divide a tela é gerado por um laço de repetição que desenha uma linha de pequenos quadrados.
Aula 07 - Relógio: resto e quociente
O desafio é criar um relógio usando o Pebble Alphabet de Clotilde Olyff.
Para isto, podemos extrair os algarismos da imagem acima manualmente e salvá-los como imagens individuais. Então, no sketch, quando quisermos exibir o dígito "1", por exemplo, carregamos a imagem respectiva e exibimos na tela.
O Processing oferece funções para capturar horas, minutos e segundos do sistema na forma de números inteiros. Porém para exibir os dígitos corretos conforme explicado anteriormente é preciso quebrar os números de dois algarismos em dígitos individuais. "12", por exemplo, deve ser quebrado em "1" e "2".
A solução é simples: dividir o inteiro por 10. Mantendo "12" como exemplo, o quociente da divisão será "1", e o resto será "2". Temos os dígitos necessários: "1" e "2". Isto é feito para horas, minutos e segundos. O resultado é este:
Como este arquivo envolve carregamento de imagens, não é possível executá-lo online.
Para isto, podemos extrair os algarismos da imagem acima manualmente e salvá-los como imagens individuais. Então, no sketch, quando quisermos exibir o dígito "1", por exemplo, carregamos a imagem respectiva e exibimos na tela.
O Processing oferece funções para capturar horas, minutos e segundos do sistema na forma de números inteiros. Porém para exibir os dígitos corretos conforme explicado anteriormente é preciso quebrar os números de dois algarismos em dígitos individuais. "12", por exemplo, deve ser quebrado em "1" e "2".
A solução é simples: dividir o inteiro por 10. Mantendo "12" como exemplo, o quociente da divisão será "1", e o resto será "2". Temos os dígitos necessários: "1" e "2". Isto é feito para horas, minutos e segundos. O resultado é este:
Como este arquivo envolve carregamento de imagens, não é possível executá-lo online.
segunda-feira, 25 de agosto de 2014
Aula 06 - Lançamento Balístico
Continuamos o simulador iniciado na quinta aula. Implementamos o movimento retilíneo uniformemente variável (MRUV), que difere-se do MRU por sofrer efeito de uma nova variável: a aceleração. A aceleração é a variação da velocidade do corpo conforme o tempo. No MRUV, a aceleração é constante.
Para reproduzir o lançamento balístico, precisamos analisar o movimento de um corpo lançado para o alto. A velocidade vertical deste corpo sofre efeito da gravidade, aceleração de 9,8 m/s² com direção vertical no sentido do chão (MRUV). A velocidade horizontal do corpo, desprezando-se o atrito do ar, não sofre qualquer efeito, portanto é constante (MRU).
O lançamento balístico é a junção destes dois movimentos: MRU na horizontal e MRUV na vertical. O resultado da aplicação das fórmulas matemáticas destes movimentos no simulador pode ser conferido aqui:
Para reproduzir o lançamento balístico, precisamos analisar o movimento de um corpo lançado para o alto. A velocidade vertical deste corpo sofre efeito da gravidade, aceleração de 9,8 m/s² com direção vertical no sentido do chão (MRUV). A velocidade horizontal do corpo, desprezando-se o atrito do ar, não sofre qualquer efeito, portanto é constante (MRU).
O lançamento balístico é a junção destes dois movimentos: MRU na horizontal e MRUV na vertical. O resultado da aplicação das fórmulas matemáticas destes movimentos no simulador pode ser conferido aqui:
terça-feira, 19 de agosto de 2014
Aula 05 - MRU
Cálculos científicos foram um dos maiores motivadores do início do desenvolvimento da computação eletrônica. O ENIAC, nascido durante a Segunda Guerra, é creditado como o primeiro computador digital de grande escala e seu objetivo primário era realizar cálculos balísticos. Mesmo com uma capacidade de processamento obviamente ínfima se comparado aos computadores atuais, o ENIAC era capaz de fazer contas muito mais rapidamente do que humanos fariam.
As simulações virtuais foram o avanço dos cálculos eletrônicos. Hoje as máquinas permitem visualizar o resultado e o processamento de cálculos complexos.
Explorando esta possibilidade, desenvolveremos um simulador de balística no Processing. Cada aula acrescentará uma característica do cálculo e de início trabalhamos com movimento retilíneo uniforme (MRU), ou o movimento de um móvel em velocidade constante em relação a um referencial ao longo de uma reta.
O resultado foi este:
domingo, 17 de agosto de 2014
Aula 04 - Repetições
Repetições em programação são códigos executados diversas vezes seguidas caso determinada condição seja atendida. As repetições mais comuns na maioria das linguagens de programação são while e for. Para desenhar uma linha de quadrados, como no exemplo abaixo, repete-se o desenho do quadrado 10 vezes utilizando o eixo X como parâmetro.
Para criar uma imagem em halftone no Processing, pode-se executar um processo parecido, desenhando círculos cujo diâmetro muda conforme o eixo Y:
Outro exemplo, levando em conta a distância de cada ponto em relação ao ponteiro do mouse (e um pouco de noise):
segunda-feira, 11 de agosto de 2014
Aula 03 - Funções
Funções matemáticas são leis que geram um elemento y correspondente para cada valor x, o velho f(x). O resultado de um conjunto de valores processados por uma função podem ser exibidos em gráficos, e isso torna as coisas bem mais interessantes:
O gráfico acima é uma imagem do gráfico gerado pelo buscador Google quando se insere a função em destaque na caixa de pesquisa.
Que tipo de desenho poderíamos fazer com uma função bem mais simples? Uma onda senoide... Ou duas ondas inversas. Ou melhor, uma sequência de DNA!
Que tipo de desenho poderíamos fazer com uma função bem mais simples? Uma onda senoide... Ou duas ondas inversas. Ou melhor, uma sequência de DNA!
quinta-feira, 7 de agosto de 2014
Aula 02 - Exemplos
O site do Processing conta com uma variedade de exemplos técnicos. Eles apresentam funcionalidades pontuais e são ótimos para entender e conhecer as capacidades da linguagem.
Modificando parâmetros e acrescentando algumas linhas de código, pode-se modificar um exemplo como este em algo bem mais irreverente:
O exemplo original apresenta um círculo que segue o cursor em uma trajetória suavizada. A velocidade de aproximação diminui conforme a proximidade, pois o deslocamento por frame é a diferença entre a posição do círculo e do cursor (multiplicado por uma razão pré-determinada).
Na modificação, o primeiro passo foi remover o redraw do background. Agora o background só é desenhado 1 vez, no setup. O círculo, que antes tinha apenas preenchimento (fill), agora tem apenas contorno (stroke), de 22 pixels. E a cor do contorno muda sempre que a posição do círculo muda. A cor é o resultado de três variáveis (RGB), onde R é modificado pela posição X do círculo, B pela posição Y, e G pela hipotenusa. Se o mouse estiver pressionado, as variáveis RGB são calculadas aleatoriamente.
Modificando parâmetros e acrescentando algumas linhas de código, pode-se modificar um exemplo como este em algo bem mais irreverente:
O exemplo original apresenta um círculo que segue o cursor em uma trajetória suavizada. A velocidade de aproximação diminui conforme a proximidade, pois o deslocamento por frame é a diferença entre a posição do círculo e do cursor (multiplicado por uma razão pré-determinada).
Na modificação, o primeiro passo foi remover o redraw do background. Agora o background só é desenhado 1 vez, no setup. O círculo, que antes tinha apenas preenchimento (fill), agora tem apenas contorno (stroke), de 22 pixels. E a cor do contorno muda sempre que a posição do círculo muda. A cor é o resultado de três variáveis (RGB), onde R é modificado pela posição X do círculo, B pela posição Y, e G pela hipotenusa. Se o mouse estiver pressionado, as variáveis RGB são calculadas aleatoriamente.
quarta-feira, 30 de julho de 2014
Aula 01 - Resenha: "Hello World! Processing"
Todos os vídeos, textos e mídias em geral que já vi a respeito de Processing, Arduino e ferramentas de programação para “não-programadores” tentam convencer o espectador entusiasta de que programar é legal e fácil com a linguagem ou ferramenta que eles propõem. O documentário “Hello World! Processing” não é diferente. Verdade seja dita: programar não é legal. O resultado do trabalho geralmente árduo de programação é que é muito legal e recompensador.
Aos vinte e três minutos, Kate Hollenbach aponta:
“One of the most important advantages of Processing is that it makes it really easy to teach programming to peole who are primarily interested in visual design and the arts. Processing makes it a lot simpler to write programs that put things on screen faster”
Para ficar OK eu só substituiria “really easy” por “easier”. Apesar de parecer que estou me contradizendo, concordo que nenhum outro ambiente de programação gratuito que conheço oferece recursos tão especializados em desenho interativo e dinâmico computacional. Portanto, o Processing ganha um ponto para este fim. E por isso, “easier”.
Casey Reas e Ben Fry afirmam que o Processing foi criado para que o sujeito com uma ideia saia do campo da imaginação e esboce-a no computador. Este sim é o ponto que considero o maior trunfo da ferramenta para quem sabe usá-la.
Nos últimos minutos o filme aborda a comunidade – usuários, desenvolvedores, contribuidores, – uma menção relevantíssima para explicar o sucesso da ferramenta.
Para um documentário, penso que “Hello World! Processing” foi conceitual demais. Deu pra entender que a linguagem foi criada para prototipar, rascunhar, descartar, desenhar, entreter, produzir... Mas falta realidade. Um exemplo muito interessante abordado no filme foi o uso do Processing para visualização de dados. Dados visuais são naturalmente mais atrativos do que tabelados. Certamente existem outras boas aplicações além desta que poderiam ter sido abordadas também. O documentário deveria ter *documentado* mais.
p.s.: a animação hipnótica da UCLA sobre “o que é computação” que aparece em trechos no filme deve ter feito muitos pré-universitários desistirem de cursar computação em 1957...!
Assinar:
Postagens (Atom)


































